https://codenme.tistory.com/22
데이터베이스 참고자료
index~ recovery system
codenme.tistory.com
위의 자료를 기반으로 작성한 내용입니다. 페이지 별로 관련 내용을 정리한 것이니, 해당 자료와 함께 보는 것을 권장 드립니다.
(update at 23-08-08)
part1
https://codenme.tistory.com/21
[DB] indexing part-1 (index의 구조)
https://codenme.tistory.com/22d 데이터베이스 참고자료 index~ recovery system codenme.tistory.com 위의 자료를 기반으로 작성한 내용입니다. Dbms가 레코드 들을 잘 찾기 위한 구조로써 heap은 별로다. (전체를 다
codenme.tistory.com
이전 글에서는 순서대로 접근해왔다, 하지만 실제는 ordered index 가 아닌, B 트리를 주로 이용한다.
이번 글에서는 B 트리, 그리고 그 발전 형태인 B+ 트리에 대해 알아보자.
Ordered Index- 문제점 및 해결책
sequential하게 record 배치하게 되면 저장된 데이터를 찾을 때 쉽게 찾을 수 있지만,
데이터가 자주 변경되면 연속성을 유지하기 어렵다. (순서 안 지키는거 따로 빼놓고, 순서 유지하게 넣어주고 빼 줘야한다.)
따라서, 데이터가 주기적으로 변하는 실제 구현에선, Order를 Sequential하게 유지하는 설계는 효율적이지 못하다.\
그래서 해결책으로 나온게 B+ 트리 구조이다.
B+ 트리 Quick OverView
노드 중간중간에 공간을 비워 놔서 새로운 데이터가 들어와도 전체를 다 reconstruction 하지 않고 흡수할 수 있도록 구성 되어 있다. ( 중간 중간 빈 공간만 정렬해서 저장 해주면된다. ) 따라서 B+트리는 데이터에 변경이 많은 상황에서 효율적이다. 대신 이걸 위해 중간중간 여유공간을 만들어야 한다 -> space overhead 발생!
B 트리 구조 도입시의 장, 단점
장점
1) Insert, delete가 부분적으로 발생
2) Insert, delete시에 자동으로 트리가 조정된다
3) BST와 비슷한 로직으로 탐색 범위 감소
4) Block I/O 횟수 적다( 트리 높이만큼만 I/O log n (search key 수) 의 높이.
단점
1) 포인터를 위한 space overhead
2) Insert, delete시 구조 변경 overhead.
B: (balance) 트리

노드 구조: B 트리의 각 노드는 키와 연결된 값 또는 데이터를 저장합니다. 모든 리프 노드는 동일한 레벨에 존재하며, 루트 노드에서부터 리프 노드까지 동일한 거리를 갖습니다.
키 중복: 중복된 키를 허용합니다.
포인터 수: 각 노드는 자식 노드를 가리키는 포인터를 포함하며, 노드당 포인터의 수가 적습니다.
탐색 성능: B 트리는 탐색, 삽입, 삭제 연산 모두 O(log n) 시간 복잡도를 가집니다.
범위 탐색: 범위 탐색에는 적합하지 않습니다. (시작~ 끝의 위치를 찾을 때, 매번 root 부터 시작해서 leaf까지 탐색해야한다.)
장점
- 데이터베이스의 인덱스로 사용하기에 적합하며, 범위 탐색이 상대적으로 빠르다.
- 중복된 키를 지원하여 데이터 중복을 허용한다.
- 데이터를 효율적으로 분산 저장할 수 있다.
단점
- 노드의 포인터 수가 적어 메모리 효율이 떨어질 수 있다( 모든 non-leaf 노드가 실제 data 값을 가지기에 공간 부족).
- 노드 분할과 병합이 빈번하게 발생하여 성능에 영향을 줄 수 있다.
2) B-Tree의 특징
- 모든 Leaves는 같은 레벨이다.
- B-Tree는 최소한의 차수 t를 정의하며 t의 값은 disk block size를 참조한다.
- 모든 루트 Node는 적어도 t-1 키개의 값들을 가지고 있으며 루트는 적어도 하나의 키값을 가지고 있어야 한다.
- 모든 노드는 적어도 2^t -1 개의 키 값들을 가지고 있어야 한다.
- 자식 노드의 수는 키 값의 +1 이다.
- 노드들의 모든 키 값들은 오름차순이다. 키 k1과 k2 값 사이의 자식들은 k1, k2 사이의 값들을 모두 가지고 있어야 한다.
- B Tree는 내부 노드의 자식의 노드 수가 증가 및 축소로 미리 정해진 범위내에서 변경가능하다.,
- 균형잡인 이진트리와 동일하게 Search, Insert, Delete 복잡도는 log(N)이다.
- B- Tree의 노드 삽입은 리프 노드에서만 가능하다.
- 모든 노드에 key, data를 통해 데이터를 저장한다
B+ 트리
우선, 간단하게 전체적인 구조를 살펴보자.

다음과 같은 인덱싱을 B+트리로 나타내면 아래 그림과 같다.

B-Tree는 보통 Self Balancing 탐색 트리라고 한다. 우리는 많은 데이터를 메인 메모리에 저장할 수 없다. 키의 숫자가 많으면 많을 수록 디스크에 I/O 하는 시간이 길어지며 B-Tree는 디스크 I/O 시간을 줄이고자 하는 알고리즘이다.
실제 DB의 인덱싱은 대부분 B+트리로 이루어져있다.
- 노드 구조: B+ 트리는 B 트리와 유사하지만, 리프 노드들이 연결 리스트로 연결되어 있습니다. 모든 키는 리프 노드에서만 저장된된다.
- 키 중복: 중복된 키를 허용한한다.
- 포인터 수: 각 노드는 자식 노드를 가리키는 포인터를 포함하지 않고, 리프 노드에서만 데이터와 관련된 포인터가 저장된된다.
- 탐색 성능: B+ 트리 역시 B 트리와 같이 탐색, 삽입, 삭제 연산 모두 O(log n) 시간 복잡도를 가진다.
- 범위 탐색: 범위 탐색에 최적화되어 있다.
장점:
- 메모리 효율이 높다.( non-leaf 노드는 실제 데이터를 가지지 않고 다음 위치를 가르키는 포인터만 보유하기에, 효율적이다.)
- 리프 노드가 연결 리스트로 구성되어 있어 범위 탐색에 유리하다( 이 글의 뒤에서 설명하겠다.).
- 데이터베이스 인덱스로 많이 사용되며, 범위 쿼리에 대한 성능이 우수하하다.
단점
- 중복된 키를 지원하여 데이터 중복을 허용한한다.
- 데이터의 분산 저장에는 B 트리보다는 적합하지 않을 수 있다.
B+ 트리의 Leaf 노드
B+트리에서 leaf노드의 마지막은 다른 leaf node 를 가르키도록 생성 된다.
이를 통해 다음 leaf 노드의 시작점 레코드를 바로 얻을 수 있다.

B+트리의 non-leaf 노드
Non-leaf node는 leaf를 가르키는 multi-level sparse index 로써 동작한다.
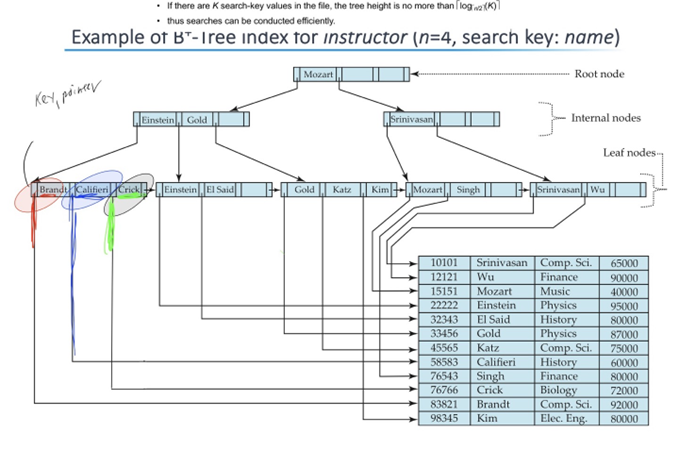
노드에서 표현하는 child가 많아질수록 tree의 높이가 낮아진다.
b+ 트리는 pointer로 inter node connection이 가능해서, logically 가까운 block 들이 physical하게 가까울 필요가 없어 졌기에, 근처에 없는 블록들도 빠르게 찾아갈 수 있다.
데이터사이즈가 아주 커져도 tree 의 높이는 크게 늘어나지 않는다. ( io 횟수가 상대적으로 조금만 늘어난다= insert, delete overhead)
B+ 트리 삽입
- 일단 key를 적절한 위치에 insert
- 이때 key가 추가된 노드에서 최대 개수(< m) 보다 작아 트리 구조 변경할 필요 없으면 그대로 끝
- 초과 시 split 수행.
B+ 트리 삭제
- 일단 key 가 위치한 leaf 가서 key 단순제거. (한칸씩 당기기)
- Key를 제거했는데 key최소 개수(m/2 이상) 만족하고,
- non-leaf(internal) 에 해당 key가 존재 x일시 ( = leaf의 leafmost에 위치한 key 가 아님)
- 단순 삭제 가능. 만약 최소 키 개수 아래> merge, merge하면 최대 개수 초과시 redistribution
B tree와 B+ tree의 차이점 비교
B+tree는 B-tree의 확장개념이다.
- b-tree와 달리 모든 노드에 key, data가 있지 않으며, leaf 노드에만 key, data가 있다 (Non- Leaf Node는 Search하여 실제 데이터가 있는 leaf에 접근하는 Key의 역할을 수행한다.)
- leaf 노드끼리는 연결리스트로 연결되어 있다. Logical 하게 보면 index sequential 과 유사하다.
Non-leaf는 leaf를 가르키는 multilevel index. Leaf는 dense index로 모든 record를 가르킨다.
Leaf는 linked list 되어 있다. 각 leaf는 정렬되어 있고, leaf 노드 도착 시, 가장 왼쪽 키부터
완전탐색으로 key를 쭉 찾아 나간다.
B-tree와 각 노드에 데이터가 저장이 되지만 B+tree의 경우엔 인덱스노드와 리프노드가 분리되어서 존재한다. 그리고, 리프노드는 서로 연결되어 있어서 임의접근과 순차접근모드 성능이 우수하다.
공통점
1. 모든 leaf의 depth가 같다
2. 각 node에는 k/2 ~ k 개의 item이 들어있어야 한다.
3. search가 비슷하다.
4. add시 overflow가 발생하면 split 한다
5. delete 시 underflow가 발생하면 redistribution하거나 merge 한다.
차이점
1. B-tree의 각 노드에서는 key 뿐만 아니라 data도 들어갈 수 있다. 여기서 data는 disk block으로의 포인터가 될 수 있다. 반면, B+tree는 각 non-leaf에서는 key와 다음 노드로 향하는 포인터만 들어가야 한다. 그러므로 B+tree에서는 실제 데이터를 가르키는 disk 액세스 주소값이 오직 leaf에만 존재한다.
2. B+tree는 B-tree와는 달리 add, delete가 leaf에서만 이루어진다.
3. B+ tree는 leaf node 끼리 linked list로 연결되어 있다.
B 트리에 대비되는 B+tree의 장점
- 블럭사이즈(노드사이즈) 를 더 많이 이용할수잇다 ( 키값에 대한 disk 엑세스 주소가 없고, 다음 노드로 향하는 포인터 정보만 가지고 있기 때문에 동일한 disk block 사이즈 기준, 더 많은 key를 넣을 수 있다.)
- leaf node 끼리 linked list로 연결되어있어서 시퀀셜한 레인지 탐색에 매우 유리하다
B 트리에 대비되는B + Tree 의 단점
- B Tree의 경우 best case에는 루트에서 끝날수 있지만(non-leaf에서 찾을 수 도 있다) , B+ Tree의 경우 무조껀 leaf노드까지 가야한다. But non-leaf에서 찾는 건 드물기에 무시 가능.
B+ 트리는 Range query에서 좋다.

시작점을 leaf노드에서 찾고, 끝지점이 나올때까지 계속해서 leaf가 가진 포인터가 가르키는 다음 leaf 지점으로 이동하면서 찾아나가면 되기에, Range query의 성능이 상당히 좋게 나온다.
Index-sequential file VS B+ 트리
Index-sequential file 의 상대적 단점
file이 커질수록 퍼포먼스 감소( overflow block이 계속 생긴다)
주기적으로 전체 파일을 reorganize 해야한다 ( 이건 매우 cost 소모하는 작업)
B+ 트리의 상대적 장점:
Tree 스스로가 자동으로 insert, delete에 대해 tree 구조 변화시킨다.
주기적으로 전체 파일을 reorganize할 필요가 없어진다.
B+ 트리의 상대적 단점( 사소하다)
Insert, delete overhead(tree modification overhead), space overhead 발생. 하지만 장점이 더 크다!
-> 대학의 과제로 on-disk B+ 트리 코드를 구현하고, tree-modification의 오버헤드를 줄이고자 key- Balancing, logical delete 적용한 프로젝트 코드가 있는데, 관심이 있다면 아래 링크를 참고하자.
https://github.com/shyswy/ComputerScienceProjects/tree/master/dbms/B%2Btree_development
주의
B+ 트리는 multi-level index 이지만, multilevel – index-sequential file과는 다르다.
Index sequential file: 인덱스를 통해 데이터 파일의 각 레코드에 접근할 수 있으며, 데이터 파일의 레코드가 정렬된 순서로 저장되어 있는 구조를 갖고 있다.
block은 key 값의 순서에 따라 실제 물리적 위치가 정렬되어 있는 레코드들의 집합이다.
Block은 고정된 수의 레코드만을 저장할 수 있기 때문에 overflow가 발생하는 경우에는 한 block을 두 개의 block으로 분리해야 한다. 아래의 그림은 block에서 overflow가 발생한 상황과 overflow를 처리하기 위해 block을 분리하는 과정을 나타낸다.

B+ 트리가 실제 구현에서 좋은 이유는?
Ex) 각 노드가 4Kb 블록일시, 블록 내의 Data 1개당 40byte 엔트리 사용한다하면 (key, pointer로 구성된 엔트리) 4kb에 약100개씩 넣을 수있다. -> 노드마다 100개의 child가지게 된다. 노드 하나마다 파생되는 노드의 수 가 많아질수록 tree의 높이가 낮아져서 성능이 상대적으로 높다. ( log 100 N > log 200 N) ( 각 노드의 자식수(100,200)에 따른 높이)
Q) search key 1000000개, n=100
n/2= 50 (추정. 2/n ~ n개)
Log50 ( 1000000) ==4 node가 root 에서 leaf까지 가는데 탐색하는 노드 수 ( 높이)
BST는 2명의 자식만. 따라서 높이가 훨씬 높다. 실제에서 1개의 node 탐색 = 1개의 I/O 발생이다. 따라서 높이는 중요한 요소!
요약
Non leaf VS leaf node
Non leaf: sparse index의 성격 -> leaf node에는 모든 데이터에 대한 표현이 되 있어야 유실된 정보가 없는 것. (10000개 리코드 존재시, search 하면 맨하단까지 내려가면 모두 있을 것! ( dense index의 성격)
leaf: dense index로 표현 되어야 하고, sort되어진다. 만약 데이터 insert 이후에 공간 있으면 정렬하게되고, 공간이 없다면 split 발생! Pointer( 시작위치 가르키는거) 가 부모노드로 올라가게 되는데, index가 추가되는 과정에서 leaf: dense index 유지되야 하기에 남겨놓고, Non-leaf에선 (sparse index) 에선 그 값이 필요 없기에 그 값을 child 노드에 남겨 놓지 않아도 된다. (여유공간이 있다면 데이터 추가, 여유공간 x 시 leaf노드부터 split > parent가 split으로 새로 생긴 자식 노드를 가르키는 포인터를 저장할 공간 있으면 할당 후 끝, 아니면 부모의 부모 …. 끝까지 간다.)
인덱스: 원하는 데이터를 빠르게 찾기 위해 모든 레코드를 뒤지지 않고 필요한 레코드만 찾기 위해, 인덱스 사용.
B+ 트리: ordered index 구조. 각 노드의 child pointer를 나타낼 때 전부 채운다 -> 반이상만 채워도 되게 -> 데이터 삽입 시 전체 소트 x 필요한 부분만 소트.
데이터를 지우게 될 노드를 리프에서, 지우고 나니 리프의 개수 조건인 [ n-1/2 ~ n-1]를 만족하지 않는다면
두 leaf 노드를 합쳐주고(merge) , parent에서 두 leaf 노드를 가르키던 두개의 포인터 중 하나를 제거한다.
문제: split 하자마자 바로 merge 하는 경우.
N=4 일시
Leaf : (4-1 /2) 의 반올림 ~ n-1 >> 2~3 개의 record
Non-leaf: (4/2)의 반올림 ~ n >>2~4 개의 포인터( 자식을 가르키는)
특수 case:
1) root는 최소 2개의 child 필요.
2) Root 가 leaf 일경우, 0~ n-1개 value 가질 수 있다.
lea
주의: 항상 leaf가 모든 record 포함하고, leftmost는 부모키와 같게하자!
단, 삭제된 record가 leaf에선 제거되도 non-leaf에선 남아있을 수도..?
Leaf의 leftmost 삭제시, 부모키를 새롭게 변경된 leafmost로 바꿔줘야한다.
B+ 트리 inset, delete 시 트리 변화 예시

Leaf에서 split시 올라가는 부모키를 자식에게 줘야한다( 모든 record 보유해야)
부모에게 키를 넘겨주면, 5개의 자식을 가지게 되기에 split 발생
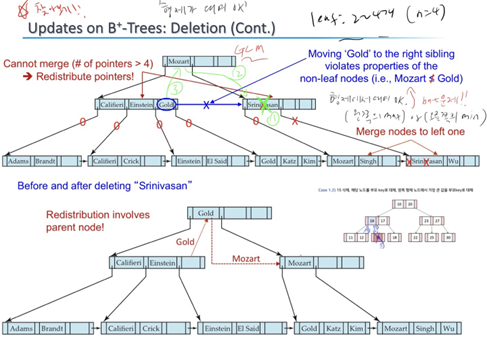
- 아래에서 key 삭제 -> leftmost기에 부모에 해당 key 존재.
- 우선 leaf가 최소조건 만족x 기에 merge 수행, 부모에 Srin 제거. -> 부모의 키가 최소조건보다 적어짐(자식 1개)>>merge or redistribution.
- root는 최소 2개의 자식 가져야한다 ( 특수 rule) >> redistribution 수행

- Leaf의 record 최소조건 위배> merge시 최대조건 위배 -> redistribution
- leaf에서의 redistribution은 이웃 노드가 부모, 삭제된 노드에 rightmost key를 주는 것.
- (leaf는 모든 record 가지고 있기에 이미 kim을 보유하고 있다)

최소 키 조건 위배 > Merge > 부모가 최소 자식 조건 위배 > merge -> root가 최소조건 ( 2 이상) 위배 > root 제거.
B+ tree File Organization
Index와 File 이 합쳐진 구조이다.
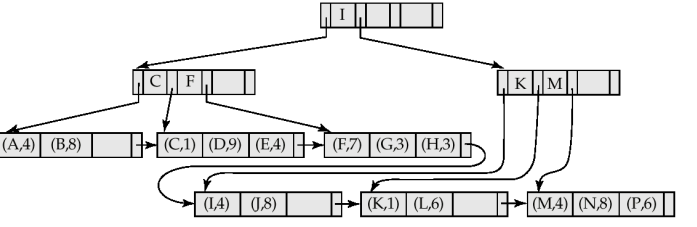
- Key, Pointer (index) -> Key Value (File)
- Pointer 대신 실제 record를 넣는다
- index가 실제 record보다 크기가 작지만, leaf 노드가 여전히 half full 구조는 유지가능하다..
- record들이 수정, 삭제, 삽입 시에도 clustered하게 유지되기에 ( 자동으로 reorganize) 기존의 overflow block 구조보다 성능이 좋다.
B-Tree Index File

B트리는 B+트리와 다르게 redundent한(중복된) 데이터를 제거한다.
또한 모든 non-leaf node의 key들이 key, 자식으로의 pointer 구조가 아닌, 각 key들이 실제 value를 가지고 있다.
B 트리 장점: leaf 까지 가지 않아도 중간에 원하는 데이터를 찾을 수 있다.
단점: 중간에 찾을 수 있는 확률이 매우 적다, insert delete가 B+ 트리보다 훨씬복잡..
B+ 트리: leaf까지 내려가야 원하는 정보 get 가능.
보통의 경우, B+ 트리가 가지는 이점이 더 많기에, 파일 구조 내에서도 B+ 트리 구조를 사용한다.
Hash Indices
순서대로 기록하지 않고, hash function으로 특정키가 위치할 곳을 표시한다.
Bucket: 1 or 다수의 엔트리 모음
Search Key -> Hash function -> bucket의 알맞은 entry 와 같은 과정을 거쳐 원하는 데이터를 찾는다.
Disk의 fixed size 한 entry에 저장, 만약 저장공간이 부족하게 되면 overflow block을 할당 받고
엔트리를 저장한 뒤, 추가된 bucket들을 linked List 형식으로 연결해둔다.
Hash function의 2가지 요소( 이걸 지켜서 만들면 좋다)
1) Uniform: 모든 key들이 여러 bucket에 균등하게 저장되게
(한군데만 뭉쳐 있게 하면 별로다)
2) Random : 실제 search key의 분포와 무관하게 bucket에 균등하게 분배해야한다.

위 그림은 bucket 당 학과단위로 저장한 것이다.( 학과이름 char 값 % 10 등으로.)
이런 식으로 각 bucket에 의미 단위를 부여한다면, 조금 더 나은 성능을 보일 수 있다.
ex) 컴퓨터 학과인 모든 학생 출력하는 경우, 1개의 버킷 내에서 전부 찾을 수 있게 된다.
Bucket Over Flow 관리하기
hash 쓰다 보면 특정 bucket에 집중 될 수 있다. -> overflow 발생 시 문제!
모든 bucket 크기 무조건 키우는 건 낭비, 데이터 사이즈를 정확히 예측하기도 어렵다.
Bucket OverFlow 해결책
1) OverFLow Chaining

close addressing: hash가 부여한 주소 그대로
Overflow block을 linked list로 쭉 붙인다.
2) Open addressing(hash function 이 할당한 주소를 변경해서 사용)

주변에 공간 여유 있는 블록에 할당 >>추가적인 block을 할당 받지 않는다. 하지만, 이 방식을 사용하면 ‘학과 단위’ 로 저장한 의미 단위가 사라진다. db에선 deletetion이 빈번하기에, 실제론 부적합하다.
static Hash, Dynamic Hash
Static Hashing: 정적 해싱에서 함수 h는 검색 키 값을 일정한(static) B 개의 버킷 주소로 매핑한다.
하지만, 데이터베이스는 시간에 따라 확장하거나 축소될 수 있다
Static hashing의 문제: 특정 bucket에만 Overflow로 인해 linked list가 계속해서 달리면? 문제
Hash는 탐색 범위를 줄이고, 거기서 찾으려고 사용하는 방법인데 효율이 나빠진다.
공간을 bucket에 맞게 적절하게 할당하기 어렵다…
Solution: periodic re-organization: overflow block들을 포함하여 다시 만들기. 너무 비용이 많이든다.
따라서 각 버킷의 사이즈가 동적으로 조정되는 Dynamic Hashing을 사용해야한다.
Dynamic Hasing: 그룹( bucket) 이 가득차면, 해당 그룹만 Split 해준다.
periodic re-organization
전체를 re-organization하면 비용이 크다.
B+트리는 전체를 re-organization 하는게 아닌 필요한 부분만 re-organization 했음.
B+ 트리는 총 데이터 개수에 따라 트리 높이가 달라지고, 탐색시간이 달라졌지만,
Hash는 그것과 무관하게 hash function 따라 달라진다.
indexing vs hashing
Hashing: record를 retrieve해야하는( 되찾아오는) 상황 or 특정 value를 가진 record를 찾을 때좋다.
ordered indices: 만약 range query가 빈번하다면 시작~ 끝 지점까지 순차적으로 탐색 가능한 Ordered Indices가 더 좋은 방법이다.
Write-optimize Index structure: sequential이 아닌, random Write가 많이 있으면 B+트리가 나빠진다. (B+ 트리는 ordered indice. Random한 write시에 다시 root부터 탐색하기를 반복해야한다.)
Random Write 비용을 줄이는 대안
Log-structured merge tree( LSM-tree)
write할 때 마다 tree를 변경하는 과정 자체가 번거롭고 많은 COST가 드는 과정이기에, 이를 줄이는 해결 방안이다.
따라서 요청되는 Write를 메모리에 계속 받아 놓는다(write만 따로 모아 놓기). 계층이 여러 개 존재 ( L0는 메모리, 나머지는 디스크에) 특정 Level 계층마다 size 제한이 있는데, size가 오버되면 다른 계층의(레벨의) 트리와 merge한다.
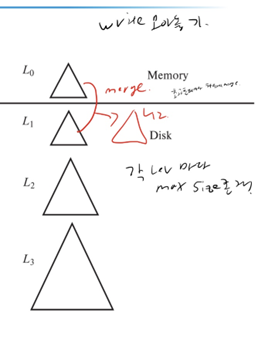
트리가 한번 생성되면, 가득 찰 때 까지 트리 변경 x, 꽉 차면 하위 레벨 트리에 한번에 merge한다.
장점
- LSM은 트리가 중간에 바뀔 경우가 많지 않기에 B+ 트리에 비해 공간을 적게 사용
단점
- 찾고자 하는 데이터가 L3에 있으면 L0>L1>L2>L3…. 전부 다 찾아야한다… worst case에서 모든 계층의 트리를 뒤져 봐야하는 단점이 존재.
- 한번씩 Tree 들을 합칠 때 마다, 엄청 큰 작업이 발생한다.
- 데이터 insert, delete 는 insert, delete 되었다는 걸 최상위 트리( 메모리 안) 에 위치와 함께 표시한다. ( 꼭 아래로 내려가서 직접 할 필요 x )
귀찮고 비용소모가 큰 Write 작업을 한번에 몰아서 처리하는 방식이다.
Buffer Tree
Internal node에 별도의 buffer을 할당한다. 버퍼에 데이터 다 모아 놓기만 하고, 버퍼가 가득차면
Child node들의 버퍼에 쪼개져서 들어간다. -> 또 차면 다시 child 의 child ….. leaf 까지 간다.

'데이터베이스(rebooting now)' 카테고리의 다른 글
| [db] transaction (1) | 2022.12.27 |
|---|---|
| [db] query optimization (1) | 2022.12.27 |
| [db] query processing (1) | 2022.12.26 |
| 데이터베이스 참고자료 (0) | 2022.12.26 |
| [DB] indexing part-1 (index의 구조) (0) | 2022.12.23 |
